Savez-vous compter ?
Les
bonnes vieilles méthodes
Ecole rue Buffon, Paris 5ème,
photographie Robert Doisneau, 1956 (auction.fr)
Quel
est le problème ?
Autrefois,
la maîtrise du calcul excéda-t-elle de beaucoup les quatre opérations ? La
France de la deuxième moitié du 19e siècle, nation de petits
entrepreneurs agricoles, artisanaux ou commerçants, enseigne à ses fils les
vertus de l’épargne, de l’accumulation du patrimoine et de sa transmission
héréditaire. Ferdinand Buisson, directeur de l’enseignement primaire de Jules
Ferry, définit la méthode : « voir
avec les yeux avant de voir avec la tête » « partir du concret pour
aller vers l’abstrait ». De
fait, les écoliers apprirent à compter en manipulant des bûchettes et en
poussant les boules de couleurs de leur boulier.
60 problèmes à la
fin de l’article, révisez vos fondamentaux…
Un
savoir lié à la nécessité économique
Le savoir-compter nécessaire
à la formation sociale reste celui du clerc de notaire : calculer une
surface foncière (ou plus exactement convertir par écrit, en système métrique,
les anciennes mesures mentales exprimées en « journaux » ou en « arpents ») ; estimer
rapidement les intérêts composés d’un capital placé à taux fixe (la rente
d’Etat ne fut-elle pas pendant longtemps la principale application des
exercices arithmétiques scolaires ?) ; récapituler la valeur de
quantités hétérogènes à des prix différents (bois en « cordes »,
grains en « quintaux », foin en « charrettes »…). Le calcul
scolaire quitte rarement le terrain des réalités matérielles familières à tous
les enfants, même ceux des familles prolétaires. Il n’est guère de nombre qui
ne s’investissent immédiatement en quantités métrologiques ou monétaires, mais
non sans difficultés supplémentaires dans beaucoup de régions de France, comme
se souvient Pierre-Jakez Hélias : « Mes
camarades et moi, nous avons quelques difficultés avec le 18 qui se dit en
breton trois-six. Nous nous étonnons un peu de ce que le Français appelle 40 ce
qui est deux-vingts, 60 ce qui est trois-vingts et pourtant, il dit quatre-vingts
comme nous. » Complication aussi des unités de compte monétaires, pour
les habitués bretons ou bisontins du « réal » : « A l’épicerie, 2 francs 15 centimes
valent en breton 8 réaux et 3 ou 9 réaux moins 2. 3 francs 10 centimes font 1
écu et 2. C’est un peu étourdissant (..). A l’école, il faut tomber tout juste.
On va chercher des grammes et des milligrammes comme les apothicaires. Ce
calcul-là est une invention d’avares ou d’hypocrites, je vous laisse à
choisir. » Le Cheval d’orgueil
Voilà, certes, un début bien
ardu, mais qui résume les avantages, le but et le caractère que prendra
l’enseignement du calcul dans les écoles primaires. Pour le reste, les
instructions ministérielles du 20 août 1857 constituent le vrai programme pour
les écoles et celles qui suivront ne diront rien de plus exact et de plus sage.
Pour atteindre ses objectifs, l’instituteur doit se servir de cette science
comme d’un moyen d’éducation, une science que l’on applique au développement de
l’intelligence, du raisonnement et du jugement de l’enfant. A lui ensuite
d’adapter ses connaissances à ses besoins, pour « calculer » avec
assurance, exactitude et facilité ce qui se présentera dans sa vie.
On considérera longtemps que, de toutes les matières du programme de l’instruction primaire, l’arithmétique est celle qui laisse le moins à désirer, appuyant ce raisonnement sur les examens du certificat d’études ou sur les concours cantonaux dont les compositions de calcul étaient généralement bonnes et les problèmes bien résolus… oubliant au passage que les élèves présentés à ces épreuves ne constituaient qu’un faible pourcentage des écoliers scolarisés, les meilleurs éléments toutefois.
La réussite au certificat, 1963
Un
vœu pieu
On peut s’interroger sur
l’application réelle de la circulaire du 20 août précitée et sa volonté de
présenter la leçon d’arithmétique comme « un
exercice de logique et morale populaires ». Ces leçons ont-elles
toujours été données avec cette simplicité et ce caractère d’utilité pratique
visant à éveiller l’intérêt de l’enfant et à lui faire acquérir « cette rapidité, cette dextérité
d’opérations techniques sans laquelle il n’aura qu’une demi-science à peu près
inutile ? » On est malheureusement gagné par le pessimisme.
Une école normale en 1865,
élèves maîtres, leur aumônier et leurs professeurs
Au milieu du 19e
siècle, même du côté des normaliens, les connaissances mathématiques se
limitaient souvent aux quatre opérations, bagage suffisant pour apprendre à
compter aux petits paysans qui vivraient, comme leurs parents avant eux, en
autosuffisance. On note d’ailleurs que la « sagesse populaire » avait
acquis une technique performante de calcul mental bien adaptée à la gestion des
activités quotidiennes.
La mécanisation alla bon
train et on assista rapidement, dans les classes, à une récitation par cœur des
définitions du nombre, de l’addition, de la multiplication et des règles qui s’y
rapportaient, tant et si bien qu’au signal du claquoir, la litanie des tables
commençait sans que l’élève ne traçât jamais un seul chiffre sur son ardoise. Pendant
deux décennies, on s’éloigna quelque peu des avancées de la fameuse circulaire
et, aussi, de l’adage de Jean-Jacques Rousseau : « Les sens sont les premiers instruments de nos
connaissances ; avant d’apprendre à l’enfant à lire, il faut lui apprendre
à voir. » L’avènement du Dictionnaire
de pédagogie de Ferdinand Buisson (entre 1881 et 1887) va rappeler la base
de l’enseignement du calcul : l’intuition. Le rôle du maître sera
d’utiliser des « moyens sensibles » afin de donner à l’écolier une
idée juste du nombre et lui éviter de « confondre
le nombre et l’idée avec les chiffres ou les signes qui n’en sont que la
représentation. »
Dictionnaire pédagogique,
Ferdinand Buisson, 1882
Bientôt, dans la deuxième
moitié de 19e siècle, le développement des techniques et
l’industrialisation du pays rendirent nettement insuffisant le savoir minimal
des maîtres et, grâce aux Ecoles normales et à leur recrutement très sélectif,
les futurs instituteurs étendirent leurs connaissances mathématiques vers des
notions plus complexes : règles de trois, pourcentages, géométrie,
fonctions…
Les
supports pédagogiques des maîtres
Au maître donc de faire
comprendre aux écoliers ce qu’est le nombre. Qu’il leur fasse compter des
objets connus ou familiers : leurs doigts, les galets collectés à la
récréation, leurs billes, le petit matériel fabriqué en classe : les
bûchettes et les jetons ; qu’il les questionne sur le nombre de tables de
la classe, sur le nombre de livres de la bibliothèque scolaire, sur le nombre
de jours de la semaine, du mois. Tout doit éveiller le sens de l'observation,
de l’attention et de la réflexion pour finalement acquérir l’« idée »
du nombre, alors, à ce stade seulement, on justifiera cette notion par des
exercices de composition, décomposition, addition et soustraction de ces
différents nombres, utilisant la foule de connaissances exactes et utiles acquises
par la manipulation. Un grand nombre d’appareils furent mis à la disposition
des apprentissages et, comme la Chine eut son souan-pan, la Russie sa schtote
et les Romains leur abacus, les
écoliers français eurent leurs bûchettes, jetons et bouliers.
Stchioty
Boulier chinois ou souan-pan (Wikibooks)
Boulier romain ou
abacus (tertisco-alexandru.com)
Boulier japonais (soroban)
Les bouliers. Le
boulier compteur, limité à des opérations simples, fut l’instrument le plus
utilisé aux débuts de l’école primaire, qu’il soit individuel ou bien
collectif. Il était peu encombrant et facile d’utilisation, mais il fut peu à
peu remplacé par les bûchettes avant de disparaître après la Grande Guerre.
Quant à lui, le boulier numérateur, inventé par Marie Pape-Carpantier (1),
était bien plus performant. Sa tringlerie permettait de représenter les classes
de nombres jusqu’aux millions… pour les écoliers de classes maternelles ! (2)
Catalogue de matériel
scolaire, Les Fils d’Emile Deyrolle, 1925
Boulier numérateur de
Pape-Carpantier
Les
bûchettes traditionnelles, puis industrielles. De
fabrication artisanale au début, préparées par le maître ou taillées par le
grand-père dans des brindilles de noisetier ou de sureau, elles devinrent,
entre les deux guerres, de belles baguettes rectilignes et colorées, avant de
faire partie du matériel décimal symbolisant les unités.
Bûchettes
« artisanales » (collection musée)
Bûchettes industrielles
(collection musée)
Toutefois, à la fin du 19e
siècle, les écoliers sortaient leur réserve de bûchettes du pupitre à l’annonce
de la leçon de calcul. De 1 à 9, ces dernières représentaient les unités, au
nombre de 10, elles étaient liées par une ficelle ou un élastique pour former
un « fagot » : 1 fagot = 1 dizaine, facile ! La suite
l’était moins, à notre fagot venait s’ajouter une nouvelle série d’unités pour
former d’autres nombres aux noms compliqués : onze, douze, treize… qui
nous amenait à un deuxième fagot et donc à deux dizaines nommées 20. Tout
allait bien jusqu’aux fatidiques 70, 80, 90 ! Bon an mal an, la fin de
cours préparatoire ouvrait la porte à la centaine. L’écolier avait découvert
tous les secrets des nombres en les composant et les décomposant et le matériel
se perfectionna, dans les années 70, avec l’arrivée des petits cubes (unités), des
dizaines (barrettes), des centaines (plaques) et les milliers (cubes), en
plastique emboîtable, la fameuse « base 10 ».
Base 10 en bois (collection
musée)
Assimilant le principe de la
numération décimale, parallèlement, l’écolier avait acquis le sens des 4
opérations : 8, c’est 5 bûchettes + 3 bûchettes, c’est aussi 6 + 2 ou 2 x
4 ou encore 9 – 1. Il s’essayait alors à la résolution de petits problèmes de
la vie courante : j’ai 5 bonbons dans ma poche (je pose 5 bûchettes sur le
pupitre), maman m’en redonne deux (j’ajoute 2 bûchettes sur le pupitre),
combien en ai-je maintenant ? Et d’entonner en cœur « 5 bonbons plus 2 bonbons = 7 bonbons », restait alors à
passer à l’abstraction de la pose de l’opération sur l’ardoise ou le cahier…
Les
jetons. Avec
les nombreuses découvertes pédagogiques initiées par les études sur la
psychologie de l’enfant, une nouvelle méthode apparut favorisant une vision
globale du nombre évitant le comptage par unité. C’est ainsi qu’à partir des
années 1930, les jetons se joignirent aux bûchettes. Plus maniables et
possédant deux faces bicolores, ils permettaient des dispositions en formes
géométriques fixant une représentation « globale » du nombre
rappelant les dominos. A la même époque, se développait aussi la fameuse
« méthode globale » de lecture. On ne pouvait cependant pas dire que
les jetons étaient une invention moderne (3).
Panneau collectif utilisant
des jetons (collection musée)
Techniques
et programmes
Le
calcul mental : Cet exercice fit les beaux jours du
procédé « Lamartinière » : l’ardoise bien à plat sur le pupitre,
la main tenant la craie levée (la droite évidemment) et prête à écrire la
réponse au son d’un coup de règle, la voix du maître énonçant clairement « Jules avait 13 billes, il en a gagné
9 à la récréation. Combien Jules a-t-il alors de billes ? » L’ambiance
est silencieuse et pesante, les yeux se lèvent au ciel, des mains (gauches
celles-là) s’agitent sous les pupitres, tentant un comptage hasardeux – coup de
règle – les mains droites s’affolent pour écrire la réponse – coup de règle – les
ardoises se lèvent au-dessus des têtes, tenues à deux mains ! Plus
question de bouger, sauf peut-être les têtes qui jettent un coup d’œil furtif
sur l’ardoise du voisin, cherchant à se rassurer quant à la réponse et
permettant une correction rapide, sans l’assurance de ne pas copier une faute… « 13 + 9 », chacun devait
pourtant savoir la technique dite et redite : « pour ajouter 9, j’ajoute une dizaine et j’enlève une unité ».
Dans d’autres situations, la parfaite connaissance des tables était
indispensable. L’entraînement se poursuivait ainsi tout au long de la scolarité
primaire, régulier et progressif, pour aboutir à l’épreuve suprême, les cinq
questions de calcul mental du certificat d’études, toutes empruntées à la vie
de tous les jours.
Les
tables : Les premiers programmes imposèrent
l’apprentissage des tables d’addition, de soustraction et de multiplication.
Seule survécut cette dernière. La rapidité de calcul et l’exactitude du
résultat des opérations dépendaient de la mémorisation de ces tables. La
hantise d’« apprendre ses tables » s’installa rapidement dans la vie
des écoliers, même s’il ne restait que la table de multiplication. Les rabâcher
le soir à la maison, les revoir le matin avant de partir, les chanter à
l’école, elles étaient partout : sur les couvertures de cahier, sur les
protège-cahiers, sur les buvards, dans les manuels… alors que certains cerveaux
rebelles en refusaient systématiquement l’enregistrement.
Les
mesures usuelles de l’école publique, laïque et obligatoire : Dès
la mise en place de l’école de Jules Ferry, la priorité fut d’unifier les
unités de mesure et d’étendre définitivement le système métrique à tout le
territoire. Chaque école fut dotée du fameux « compendium métrique »,
entendez la petite armoire vitrée qui trônait dans les classes et renfermait
les principaux instruments de mesure qu’il faudrait désormais maîtriser.
Compendium dans son armoire
Chaîne d’arpenteur
(décamètre)
Mètre à ruban (décamètre),
1890
On y trouvait,
pêle-mêle : la chaîne d’arpenteur et différents mètres (règle en bois
rigide, mètre pliant à 5 ou 10 branches, mètre en métal, mètre en ruban), la
balance romaine, la balance Roberval (4) avec sa boîte de poids en laiton
et quelques poids en fonte de 1/2, 1 et 2 kilogrammes (5), les mesures de
capacité en fer et en bois, les volumes en bois (cube, pyramide, cône,
cylindre…), tous ces objets de mesure que l’on retrouvait dans la vie courante,
notamment chez les commerçants et les artisans.
Tableau mural A. Colin,
Système métrique par Léon Vaquez, vers 1890
Volumes en bois, 1890
(collection musée)
Le système métrique : C’est la Convention qui avait décidé de l’unification des poids et mesures en 1795, instituant l’usage obligatoire du système métrique (6). Guizot, par sa loi de 1833, avait, à son tour, rendu l’apprentissage du système métrique obligatoire dans les écoles. Finalement, près d’un siècle après la Révolution, les campagnes comptent toujours en livres, en onces, en aunes, en chopines, en brasses ou en cartonnées et, évidemment, ces mesures n’avaient pas la même valeur d’une région à l’autre… L’obligation fait donc son retour avec Jules Ferry, tout comme le « seul l’usage du français est autorisé à l’école » (article 16 du règlement départemental de Saône-et-Loire de 1890).
Règlement départemental de
1890 (collection musée)
Règlement départemental de 1890, détail (collection musée)
La logique
et le rationnel semble l’emporter avec l’association du système métrique
et du système décimal avec une unité principale pour chaque mesure.
Désormais, l’écolier
mesurera les longueurs en mètres, les poids en grammes, les capacités en
litres, le tout agrémenté de multiples : déca (10 fois), hecto (100 fois),
kilo (1 000 fois), et de sous-multiples : déci (1/10), centi (1/100),
milli (1/1 000).
Déclinaison moderne du mètre
(wikipedia)
Alors commença le calvaire
des conversions : ajouter 1, 2 ou 3 zéros, déplacer une virgule vers la
droite (pour obtenir des unités plus petites) ou vers la gauche (pour obtenir
des unités plus grandes), remplacer les unités manquantes par des zéros. Facile
à priori, mais c’était sans compter sur les pièges tendus par le maître. A
peine ces notions assimilées, arrivaient les mesures de surface et de volume ! Et voilà le nombre de zéros à ajouter, doublé
ou triplé, les déplacements de la virgule qui passent d’un rang à deux ou trois
à chaque changement d’unités… Pas de quoi dissiper l’angoisse des fractions qui
arrivent !
La géométrie : Pas
de problèmes sans calcul de périmètres, de surfaces ou de volumes. Pas de
travail manuel sans découpages de carrés, de triangles, de rectangles, de
trapèzes, de cercles, ni sans constructions de cubes, de parallélépipèdes, de
cônes ou de pyramides, sans oublier le tracé et la mesure des angles.
Conclusion : il fallait apprendre par cœur les formules de calcul pour
ainsi affronter tous les problèmes qui se poseraient dans la vie quotidienne.
Règle et compas, vers 1890
(collection musée)
Matériel collectif du
maître, vers 1960 (collection musée)
Matériel de l’élève, vers
1960 (collection musée)
Les problèmes,
justement : Si seulement connaître les notions
arithmétiques sur le bout des doigts, et maîtriser parfaitement le savoir-faire
opératoire suffisaient pour tout résoudre… Quid de la « bosse des
mathématiques » et du raisonnement logique ? Heureusement, les
instructions officielles ne préconisaient que la résolution de problèmes
simples de la vie courante qu’un entraînement répétitif suffirait à installer des
automatismes. D’accord pour savoir ce qu’avait encaissé la fermière qui vendait
3 douzaines d’œufs au marché, à 0 franc 50 la douzaine. Mais si elle avait
aussi vendu 4 poulets à 3 francs 50 l’un, et 6 fromages à 2 francs 75 les
deux ? Comment savoir combien il resterait de surface de pré à un paysan
s’il creusait une mare de 5 mètres de diamètre et 1,50 mètre de profondeur sur
un terrain de 175 mètres de long sur 66 mètres de large ? Facile pour les
uns, compliqué pour d’autres.
Alors que les instructions
parlent « de problèmes simples de la vie courante », il n’en reste
pas moins que la vie courante ne l’entend pas de cette oreille. Que
d’imprévus ! Que de situations complexes nécessitant une lecture
« fine » de la part de l’écolier ! Tout devient source
d’interrogation : et si le champ du paysan n’avait pas des formes
régulières ? Et si la fermière cassait des œufs avant de les vendre ?
Et si le cycliste était victime d’une crevaison qui faisait baisser sa moyenne,
et si les trains ne partaient pas à l’heure, et si le partage des dépenses ou
des bénéfices ne se faisait pas à parts égales… De fait, les manuels
d’arithmétique s’en donnèrent à cœur joie, on reste coi devant le nombre et la
diversité des situations inventées par les auteurs, situations qui, parfois,
dépassaient l’entendement, à l’image du 1300
problèmes, recueil de problèmes qui inventa des trains qui se poursuivaient
et des robinets qui fuyaient dans des baignoires qui se vidaient…
1300 problèmes, édition 1965
(collection musée)
1300 problèmes, édition
1965, table des matières (collection
musée)
La clarté de la réponse à un
problème se traduisait par une parfaite présentation des résultats de la
réflexion. Les exigences des maîtres étaient dictées par les instructions, dans
toute la France, elles se répétaient dans les cahiers de tous les écoliers. Un
énoncé proprement recopié, une petite colonne à droite de la page comportant
les opérations effectuées (et la preuve par 9), à gauche, la colonne principale
était réservée au développement et aux explications des étapes du
raisonnement : une phrase annonçait chaque calcul, suivie d’une opération
en ligne (à laquelle devait correspondre une opération posée en face) et d’une
réponse avec l’unité concernée. Rien n’avait changé depuis l’édition, au début
du 20e siècle, du manuel Arithmétique
de Maurice Royer et Planel Court. Cet ouvrage, qui répertoriait, par niveau,
6 650 problèmes, avait été le fruit d’une concertation entre professeurs
et préparait évidemment au certificat. Le certificat ! Avec sa terrible
épreuve de dictée qui pouvait enlever radicalement tout espoir, mais aussi la
redoutable épreuve d’arithmétique pour laquelle le 20/20 était pratiquement
inaccessible… Seuls quelques-uns avaient le potentiel pour réussir de
brillantes études mathématiques. La plupart, malheureusement poussés par des
conditions de vie modestes, n’auraient que l’ambition de reprendre la ferme
paternelle, avec toutefois les armes nécessaires qui leur permettraient
d’affronter la révolution agricole de la 2e moitié du 20e
siècle. Pour les sans-grades, ils avaient cependant appris à raisonner,
calculer et trouver, tant que faire se peut, la solution aux « problèmes
de la vie courante ».
Manuel d’arithmétique
Royer-Court, cours moyen 1ère année, 10e édition Armand
Colin, 1934 (collection musée)
Les
problèmes : terrain de jeu ou terrain miné ?
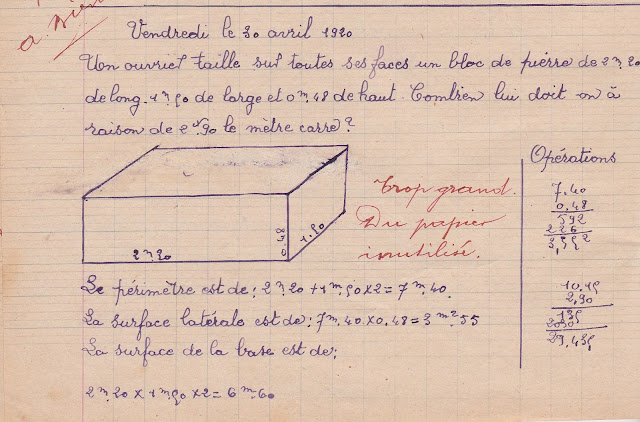
Pour illustrer et clore
notre propos sur le « savoir compter », voici les problèmes posés à Antonin,
élève de 13 ans, en classe de fin d’études. A noter que tous ces problèmes sont
extraits du fameux manuel Arithmétique et
figurent, d’une part, dans 3 cahiers journaliers (extraits présentés) et d’autre
part dans deux cahiers dits « répertoires » qui devaient servir d’aide-mémoire
en vue des révisions du certificat. La période s’étend du 3 mars 1919 au 23 juin
1920 et concerne les problèmes n° 438 à 516 de l’ouvrage. Tout cela sent bon la
campagne de notre douce France…
Tout
apprendre avant le certificat d’études
L’école de Jules Ferry
devait apprendre à la majorité des enfants, avant 13 ans, « tout ce que l’on ne doit pas ignorer ». Ce fut le règne
de l’entraînement et du « rabâchage », certes, mais avec une
progression toute militaire dont le redoublement était la règle. A la fin du
cours préparatoire, la technique des 4 opérations devait être maîtrisée avec
les nombres entiers à 2 chiffres, avec ou sans retenue. Au fil des classes
suivantes, années après années, les « entiers » augmentaient le
nombre de leurs chiffres. A point nommé, arrivaient les nombres décimaux et
leur virgule, les nombres complexes faisaient leur apparition, enfin suivis des
nombres fractionnaires, de la règle de trois et des racines carrées. Quel
programme ! Mais combien
d’écoliers, laissés au bord du chemin… qui ne subiraient jamais les épreuves
fatidiques du certif ?
En 1890, Léon Bourgeois
demande la suppression du caractère éliminatoire de la dictée afin de donner
les mêmes chances de réussite aux « matheux », en vain. Les institutrices
et instituteurs continueront donc à mettre un point d’honneur à ne présenter à
l’examen que les élèves ayant de fortes chances de réussir. Toutes les
statistiques que l’on peut trouver ne portent donc que sur les candidats
présentés. Ces dernières avançaient des taux de réussite dépassant les 60 %.
Statistiques
1965
Dans la
réalité, jusqu’en 1900, la proportion des élèves d’une classe d’âge ayant eu le
certificat varie entre 25 et 30 %. Dans les années 20, le pourcentage monte
jusqu’à 35 % pour atteindre 50 % à la veille de la Seconde Guerre mondiale. On note
déjà que ce sont les enfants d’ouvriers et d’agriculteurs qui réussissent le
moins bien à l’épreuve entre 1885 et 1940.
(1) :
Voir l’article du blog :
https://musee-ecole-montceau-71.blogspot.com/2017/10/marie-pape-carpantier-pedagogue-et.html#more
(2) : Voir les articles du blog :
https://musee-ecole-montceau-71.blogspot.com/2017/10/le-boulier-numerateur.html#more
https://musee-ecole-montceau-71.blogspot.com/2018/11/les-bouliers.html#more
(3) : « Je ne sçais compter ny à ject ny
à plume ». Ainsi s’exprimait le
grand Montaigne.
Gravure sur bois qui sert de
frontispice au chapitre Arithmétique
de Margarita, 1503
Gravures sur bois, 15e
siècle, Les
abacistes à jetons (math-rometus.org)
Il est peu probable que
Montaigne ne sut pas compter… Toutefois, dans cette phrase, il fait référence à
deux méthodes de calcul qui s’opposèrent à son époque : les abacistes qui
utilisaient des abaques à jetons (ject) et les algoristes qui commençaient à
utiliser le calcul écrit avec les chiffres indo-arabes (opérations posées à la
plume).
(4) :
Voir l’article du blog :
https://musee-ecole-montceau-71.blogspot.com/2018/09/gilles-personne.html#more
(5) : Voir l’article du blog :
https://musee-ecole-montceau-71.blogspot.com/2016/11/lecompendium-metrique-lunification.html#more
(6) : Voir l’article du blog :
https://musee-ecole-montceau-71.blogspot.com/2018/02/le-systeme-metrique.html#more
Sources :
- Les
premières leçons de calcul, Revue
pédagogique, article de T. Frieh, 1881
- Cent ans d’école, publication musée.
- Le boulier numérateur de Marie
Pape-Carpantier, Jean-Claude
Régnier, Université Lumière, Lyon 2-UMR-5191-CAR












































































































Aucun commentaire:
Enregistrer un commentaire